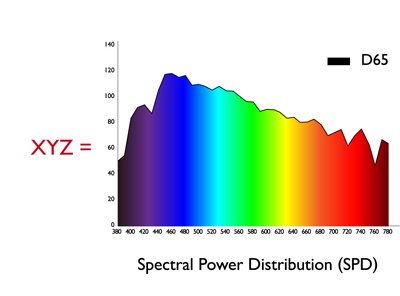
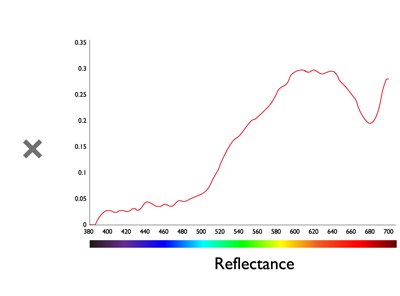
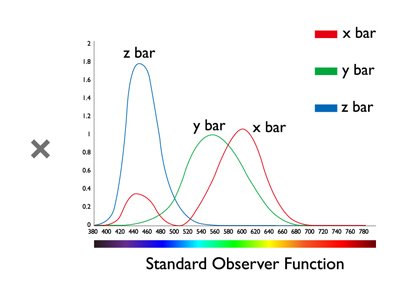
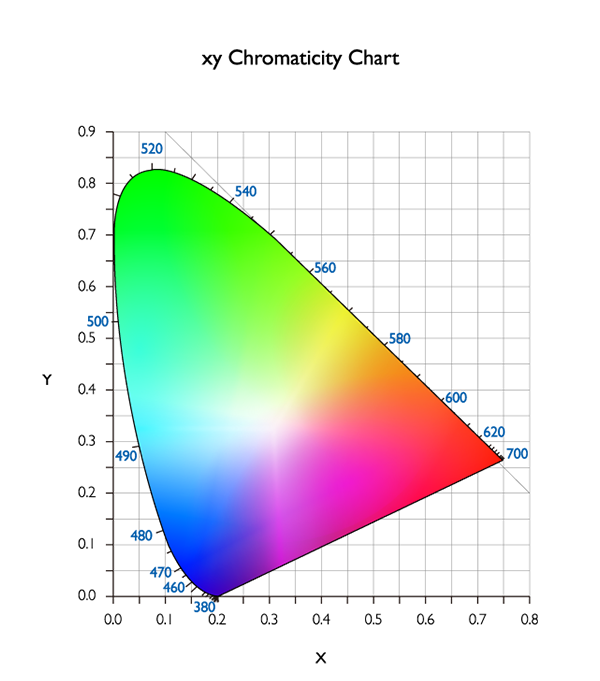
Projektor
Utforska alla Projektorserier
Efter Funktion
Home EntertainmentEfter Mest eftersökta ord
4K UHD (3840×2160) Kort Kast 2D, Vertikal/Auto Horisonal Keystone LED Laser Med Android TV Med Low Input Lag
Bildskärmar
Utforska alla bildskärmsserier
Efter Funktion
Fotografi Design Bildskärmar för MacBook BenQ Eye-care Technology | BenQ Europe On Camera MonitorEfter Mest eftersökta ord
4K(3840x2160) Med HDR 21:9 Ultrawide USB-C Thunderbolt P3 Med HöjdjusteringsstativArbete och lärande på distans