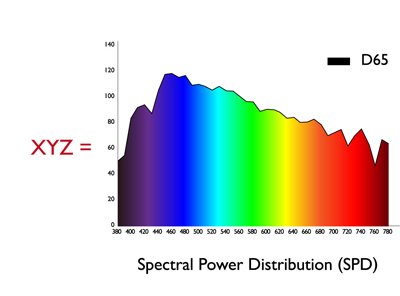
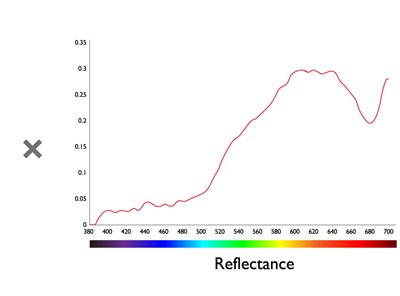
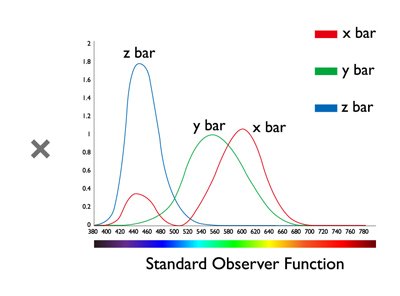
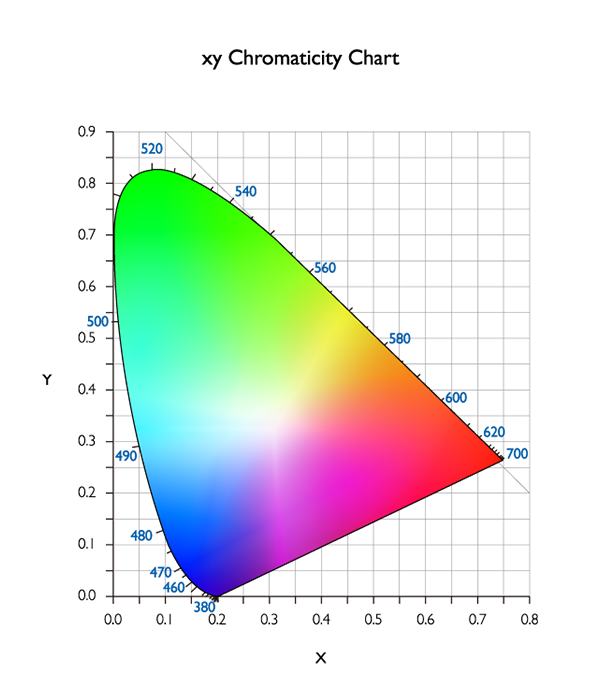
Projectors
Explore All Projector Series
By Features
Home EntertainmentRemote Work & Learning